Solving Sudoku Puzzles with a Brute-Force Algorithm
Introduction
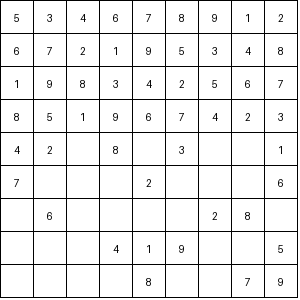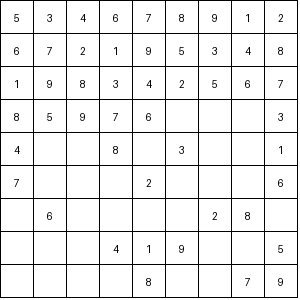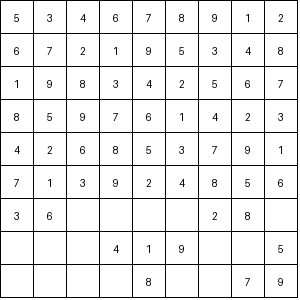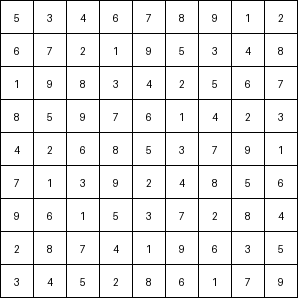
Sudoku is a popular number puzzle that challenges the solver to fill a 9x9 grid so that each column, row, and 3x3 subgrid contains all digits from 1 to 9. While many techniques can solve Sudoku puzzles efficiently, the brute-force algorithm guarantees a solution by systematically trying every possibility.
Link
Code can be found on the Github Repository
Brute Force Algorithm
The brute-force algorithm solves Sudoku puzzles by trying every possible combination of numbers in each empty cell until the puzzle is solved. Here’s how it works:
- Identify Empty Cells: The algorithm begins by locating the first empty cell in the grid.
- Try Possible Numbers: It tries placing each number (from 1 to 9) in the empty cell, checking if it fits with the existing numbers in the same row, column, and subgrid.
- Recursion for Next Cell: If a number fits, the algorithm moves to the next empty cell and repeats the process.
- Backtrack if Stuck: If placing a number leads to a contradiction later, the algorithm backtracks by removing the number and trying the next possibility.
The process continues until the entire grid is filled correctly or all possibilities are exhausted.
Recursion and Tree Structures
Recursion
Recursion is a powerful technique where a function calls itself to solve smaller instances of the problem. In the brute-force Sudoku solver, recursion is used to handle the placement of numbers:
- Base Case: When all cells are filled correctly, the puzzle is solved.
- Recursive Case: For each empty cell, the algorithm attempts to place a number and recursively solves the next cell.
Tree Structures
The brute-force approach can be visualized as a tree structure:
- Nodes: Each node represents a state of the Sudoku grid with a specific number placed in a cell.
- Branches: Each branch represents a choice of placing a number in an empty cell.
- Leaves: Leaf nodes are either solved puzzles or states where no valid numbers can be placed (leading to backtracking).
Efficient Data Storage with Bits
Efficient data storage is crucial for performance in brute-force algorithms. In Sudoku solvers, bits are used to represent possible values for each cell. For instance, a 9x9 grid can be represented using 9 bits per cell, where each bit indicates whether a number (1 to 9) can be placed in the cell.
Bit Representation
- Bitmask: A bitmask like
101001011represents possible numbers for a cell. Each bit corresponds to a number from 1 to 9, where a bit of 1 indicates that the number is a possible candidate. - Logical AND Operation: Logical AND operations are used to filter out invalid numbers based on the constraints of rows, columns, and subgrids.
Code
/* Sudoku Puzzle Solver
Solves any Suduko puzzle.
Created by Evan Loughlin - 2018.07.25
______________________________________
Usage: run ./sudoku <inputName.txt>
The input.txt file is the Sudoku puzzle to be solved, taking the following form:
5 3 0 0 7 0 0 0 0
6 0 0 1 9 5 0 0 0
0 9 8 0 0 0 0 6 0
8 0 0 0 6 0 0 0 3
4 0 0 8 0 3 0 0 1
7 0 0 0 2 0 0 0 6
0 6 0 0 0 0 2 8 0
0 0 0 4 1 9 0 0 5
0 0 0 0 8 0 0 7 9
Note that 0's indicate blanks in the input.
Keep the input.txt file in the same folder as the executable.
*/
#include <iostream>
#include <vector>
#include <bitset>
#include <fstream>
#include <cstdint>
#include <QString>
#include "SudokuPuzzle.h"
#include "SudokuCell.h"
using namespace std;
class puzzle
{
public:
// Matrix = Initial sudoku puzzle (input)
vector< vector<int> > matrix;
// Avail = matrix of 9-bit binary integers indicating possible numbers for each cell
vector< vector<int> > avail;
// Solution = Solution to puzzle (output)
vector< vector<int> > solution;
// List of pseudo-indices of all cells which are empty
vector< int > emptyCells;
bool solved;
puzzle(vector< vector<int> > vals)
{
// Convert input values to 9-bit unsigned ints
for(int i = 0; i < 9; i++)
{
for(int j =0; j < 9; j++)
{
if(vals[i][j] != 0)
{
int temp = 1;
for(int k = 1; k < vals[i][j]; k++)
{
temp = temp << 1;
}
vals[i][j] = temp;
}
}
}
this->solved = false;
this->matrix = vals;
this->solution = vals;
// Complete the matrix of available bits
this->avail = vals;
for(int i = 0; i < vals.size(); i++)
{
for(int j = 0; j < vals[i].size(); j++)
{
if(vals[i][j] == 0)
{
updateAvailableNums(i,j);
int pseudoIndex = i*9 + j;
this->emptyCells.push_back(pseudoIndex);
}
else
avail[i][j] = 0;
}
}
}
// Recursion to solve the puzzle (trying available
//combinations until a complete solution is found)
void solve()
{
//this->printEmptyCellIndices();
this->solve(0);
}
void solve(int counter)
{
// Base Case: If all empty cells have been filled, solution is found.
if(counter == this->emptyCells.size())
{
this->printSolution();
this->solved = true;
return;
}
int currentCellPseudoIndex = this->emptyCells[counter];
int i = currentCellPseudoIndex / 9;
int j = currentCellPseudoIndex % 9;
// Increment counter
counter++;
// Re-determine available numbers for current cell
updateAvailableNums(i,j);
int currentAvail = avail[i][j];
// cout << "Cell " << counter << " of " << this->emptyCells.size() - 1 << endl;
//bitset<9> x(currentAvail);
//cout << x << endl;
for(int k = 0; k < 9; k++)
{
if(currentAvail == 0 || solved)
break;
// If least significant bit is 1...
if(currentAvail & 1)
{
this->solution[i][j] = (1 << k);
//cout << " k = " << k << endl;
solve(counter);
}
currentAvail >>= 1;
}
// If all available numbers for a given cell have been tried,
// backtracking is necessary. Reset current cell value to 0.
this->solution[i][j] = 0;
}
// Updates the avail matrix for a given cell, with bits for all available numbers in a given cell.
// For example: 001000101 indicates 1, 3, and 7 are still available.
void updateAvailableNums(int rowIndex, int columnIndex)
{
int usedNums = 0b0;
// Logical OR each sudoku value in row
for(int k = 0; k < 9; k++)
usedNums |= this->solution[rowIndex][k];
// Logical OR each sudoku value in column
for(int k = 0; k < 9; k++)
usedNums |= this->solution[k][columnIndex];
// Logical OR each sudoku value in current quadrant
// Where a 'quadrant' is defined as the 9 numbers in one of 9 sections:
// [ ] [ ] [ ]
// [ ] [ ] [ ]
// [ ] [ ] [ ]
int rowLowerIndex = (rowIndex/3)*3;
int columnLowerIndex = (columnIndex/3)*3;
for(int i = rowLowerIndex; i <= rowLowerIndex + 2; i++)
for(int j = columnLowerIndex; j <= columnLowerIndex + 2; j++)
{
usedNums |= this->solution[i][j];
}
// temp currently represents all 'taken' numbers.
// Available numbers will be the negation (bit flip) of temp.
int unusedNums = ~usedNums;
this->avail[rowIndex][columnIndex] = unusedNums;
}
// Checks validity of input puzzle. Loops through every cell to find contradictions
bool puzzleInputValid()
{
//Check for row contradictions
for(int i = 0; i < 9; i++)
{
int cumulativeUsedNumbers = 0b0;
for(int j = 0; j < 9; j++)
{
if(this->matrix[i][j] == 0)
continue;
int nextUsedNumbers = (cumulativeUsedNumbers | matrix[i][j]);
if(cumulativeUsedNumbers == nextUsedNumbers)
return false;
else
cumulativeUsedNumbers = nextUsedNumbers;
}
}
//Check for column contradictions
for(int j = 0; j < 9; j++)
{
int cumulativeUsedNumbers = 0b0;
for(int i = 0; i < 9; i++)
{
if(this->matrix[i][j] == 0)
continue;
int nextUsedNumbers = (cumulativeUsedNumbers | matrix[i][j]);
if(cumulativeUsedNumbers == nextUsedNumbers)
return false;
else
cumulativeUsedNumbers = nextUsedNumbers;
}
}
//Check for quadrant contradictions
for(int k = 0; k < 9; k++)
{
int rowLowerIndex = (k/3)*3;
int columnLowerIndex = (k%3)*3;
int cumulativeUsedNumbers = 0b0;
for(int i = rowLowerIndex; i <= rowLowerIndex + 2; i++)
{
for(int j = columnLowerIndex; j <= columnLowerIndex + 2; j++)
{
if(this->matrix[i][j] == 0)
continue;
int nextUsedNumbers = (cumulativeUsedNumbers | matrix[i][j]);
if(nextUsedNumbers == cumulativeUsedNumbers)
return false;
else
cumulativeUsedNumbers = nextUsedNumbers;
}
}
}
return true;
}
void printInput()
{
cout << "=========================" << endl;
cout << " Puzzle Input: " << endl;
cout << "=========================\n" << endl;
for (int i = 0; i < 9; i++)
{
for(int j = 0; j < 9; j++)
{
int decimalValue = 0;
int binaryValue = this->matrix[i][j];
for(int k = 1; k <= 9; k++)
{
if(binaryValue & 1)
decimalValue = k;
binaryValue = this->matrix[i][j] >> k;
}
if(decimalValue == 0)
cout << "_";
else
cout << decimalValue;
if(j == 2 || j == 5)
cout << " ";
cout << " ";
}
cout << "\n";
if( i == 2 || i == 5)
cout << "\n";
}
cout << "\n";
}
void printSolution()
{
cout << "=========================" << endl;
cout << " Solution: " << endl;
cout << "=========================\n" << endl;
for (int i = 0; i < 9; i++)
{
for(int j = 0; j < 9; j++)
{
int decimalValue = 0;
int binaryValue = this->solution[i][j];
for(int k = 1; k <= 9; k++)
{
if(binaryValue & 1)
decimalValue = k;
binaryValue = this->solution[i][j] >> k;
}
if(decimalValue == 0)
cout << "_";
else
cout << decimalValue;
if(j == 2 || j == 5)
cout << " ";
cout << " ";
}
cout << "\n";
if( i == 2 || i == 5)
cout << "\n";
}
cout << "\n";
}
};
int main(int argc, char * argv[])
{
fstream fs(argv[1], std::fstream::in);
vector< vector<int> > values;
int temp = 0;
for(int i = 0; i < 9; i++)
{
vector<int> row;
values.push_back(row);
for(int j = 0; j < 9; j++)
{
fs >> temp;
values[i].push_back(temp);
}
cout << "\n";
}
fs.close();
puzzle * myPuzzle = new puzzle(values);
myPuzzle->printInput();
if(!myPuzzle->puzzleInputValid())
{
cout << "Sudoku Puzzle - Invalid Input!" << endl;
return 0;
}
myPuzzle->solve();
}
Conclusion
The brute-force algorithm for solving Sudoku puzzles is a straightforward yet computationally intensive method that guarantees a solution. By employing recursion, tree structures, and efficient data storage techniques with bits, it systematically explores all possible solutions to find the correct one.
For a detailed implementation and further exploration of Sudoku solving techniques, visit the SudokuSolver GitHub repository.




Comments